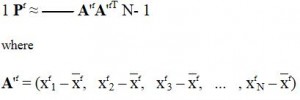An online course for PhD students and early stage researchers developed by Ross Bannister and Stefano Migliorini (NCEO) and Bethan Harris (Assimila) for the European Space Agency Data Assimilation Projects.

The Ensemble Square-Root Kalman Filters is a specialised version of a general Kalman Filter, designed for use in fields where you have big data – such as Earth Observation. The course begins with general Kalman Filters and works up from there to a full derivation of the equations for Ensemble Square-Root Kalman Filters.

Introduction

A Kalman filter is a method of data assimilation. Data assimilation is necessary because neither direct measurements nor model predictions of a physical process can ever be completely perfect.

Measurements of a physical system are always limited – sensors may be poorly placed, measurements may be lost due to external factors and the instruments themselves cannot be perfect. As well as this, measurements are also physically restricted by the time, space and money that would be required to measure a system in perfect detail.

Forecasting models, on the other hand, are large computer programs and as such they are computationally limited by cost. Weather modellers generally cannot afford to resolve the wind from every butterfly-wing flap; even though this would allow them to calculate whether these tiny gusts would grow into big storms.

The physics of the models may also require approximations and parametrisations to be made in order to represent processes that are not well understood or resolved by modellers. And even if infinitesimal resolution and complete physics were possible, the initial conditions of the model are taken from observations which – as we’ve just described – are imperfect. Errors introduced by these imperfections will grow as the model forecast progresses.

The Kalman filter is represented by a set of equations that take information from observations and combine it with models to calculate the most likely state of the system. It also calculates the probability of this state being the truth.

 Kalman filter: Earth observation example

In this example we will use a complex yet imperfect model to predict changes in ground and air temperature at an atmospheric observatory based at the University of Reading in the UK. The piece of ground that we’re specifically interested in is the car park outside the NCEO building. At each timestep we will use a model to calculate temperature changes and then incorporate observations to improve our prediction of temperature for the next timestep.

The observations

Before we look at the model let us look briefly describe the observations.

The observations are taken from a facility on the university campus called the atmospheric observatory. The ground temperature of the car park is given by the ground temperature over concrete and the air temperature is given by the dry bulb temperature. The data itself is downloadable from here.

Generally in Earth observation we are dealing with satellite measurements, to replicate this somewhat in our ground temperature measurements we will combine the temperature values recorded over three different media: concrete, soil and grass. To roughly represent the typical landscape of southern England where the university campus lies we average these assuming that we have 20% concrete, 75% grass and 5% soil.

This complete example has been written up into a Python program, which you can use to look at the results and follow along with the descriptions later on. The python program can be downloaded here.

Model and theory

Now we describe a slightly complex yet far from perfect model to predict the temperature changes that we’re going to see over the concrete ground.

As the sun drives all but the tiniest temperature changes on Earth, it is logical to use this as the starting point for our model. First we calculate the amount of solar radiation arriving at the top of the Earth’s atmosphere using the following equation,

The detailed theory of the EO Kalman Filter model and the notations used throughout this training module can be downloaded from the links on this page.

Kalman filter

Here we step through the Kalman filtering process, explaining the equations and their principles using words and imaginary wavy hands. The process involves 7 steps and the detailed theory can be downloaded here.

This technique analyses covariances and state vectors, these are then used as the initial conditions for the next timestep of the model as we run through the equations again until the end of the model run.

If we don’t have observations to add to the Kalman filter at a particular timestep then we only perform the first two calculations of the series and then use the forecasted state vector and covariance matrix on the subsequent timestep.

Look at the output of the Python code and play around with the variables to see the Kalman filter in action on this example.

The model that we used in the example on the last pages was very simple indeed – we assumed that the atmosphere is a uniform slab of air between the sun and the surface and could be fully described by the temperature of the slab and the temperature at the surface – this is clearly not true. We left out clouds, wind, precipitation, radiative scattering, atmospheric composition etc. In fact, we ignored most things about the climate system.

Our model works as an example, but it is deeply inadequate when it comes to making the real forecasts that Earth observation scientists must make. The models used in the day to day work EO have to take all of these missing processes (any countless others) into account. To make a forecast they must calculate the relationships between hundreds of different variables in thousands of gridcells timestep after timestep; as well as this they must incorporate a myriad of observations from different platforms into these forecasts to keep them as accurate as possible.

The scale of these models presents a big problem for the Kalman filter that we have described on the previous pages – with thousands of different variables and observations the covariance matrix P^f quickly becomes enormous. In sophisticated climate models you typically need around 10⁷ variables to describe the weather on a grid covering the Earth’s atmosphere. As we have seen, the P^f matrix is the square of this size – so it has to hold around 10¹⁴ pieces of information which is then used an manipulated throughout each run of the Kalman filter.

This kind of number crunching is simply beyond the capacity of current technology. As a result, many different simplifications and adaptations of the Kalman filter have been produced over the years. The Ensemble Square Root Kalman Filter is a particular flavour of these that is frequently used in Earth observation. We will describe below roughly how this filter works and what makes it different. The full calculations are worked through below.

The Ensemble Kalman Filter

The first step is to understand the usefulness of model ensembles in reducing the number of calculations to be made. The function of the covariance matrix P^f is to define the uncertainty in the forecasted system, but an ensemble of model runs provides us with an alternative way of ascertaining this: we can use the covariance between model runs instead. As long as the number of ensemble runs is considerably less than the number of variables in the state vector then ascertaining uncertainty this way is much more practical.

The equations for the Ensemble Kalman Filter are the almost exactly the same as those for the straightforward Kalman Filter from previous pages, but the Covariance Prediction is found by the following equation:

So instead of using the error of the model and updating from previous estimates, P^f is found by calculating the average spread of results across all ensemble members. This method makes some compromises made for the sake of accuracy – that is why the equation above is only approximate.

The Ensemble Square Root Kalman Filter (EnSRKF)

You may have noticed that our Ensemble Kalman Filter still contains a fairly big covariance matrix, and this must be carried and manipulated through the Kalman Filter equations. To reduce the cost of the calculations even further, many extensions have been made to the Ensemble Kalman Filter – the Ensemble Square Root Kalman Filter (or EnSRKF for short) is a one that is commonly used in Earth observation science.

One of the features of the EnSRKF is that rather than performing Kalman filtering individually on each of the ensemble members, the square root method performs Kalman filtering on the whole ensemble all at once. EnSRKF treats the ensemble as though it were one entity.

The term “square root” requires some explanation. A “square root” of the ensemble covariance matrix is considered to be the matrix of state variable anomalies – as shown in the equation above, the immediate relevance of this may not be obvious but you will see it in action on the next page. We can show this feature more obviously by writing the above equation again using matrix notation:

On this page we will derive the equations for the EnSRKF. One method that we use here but don’t describe is finding eigenvectors and eigenvalues for matrices. Most computer languages which can perform scientific analysis (e.g. Python, Matlab, R, etc) will have eigen- functionality built into them, this video and this page are a couple of good starting points if you want to find out more.

The Ensemble Square Root Kalman Filter is ultimately made up of only two equations, whose results joined together give you a single term which describes the states of all the ensemble runs at your current timestep. This is a departure from the series of equations that we have been stepping through up until now.